|
| | Mesure de vitesse au pendule balistique |  |
|
+20Xam Satanduparadis tozoz TITISSE76 Master of the skies ICE le Belge.177 Papy Aporie21 goten loisirs-optique zac Didier Shura Lepigeon marceau Ka-POW! Loulator Admin neoliv Pierre 24 participants | |
| Auteur | Message |
|---|
Admin
Pilier



 
Nombre de messages : 32648
Age : 47
Localisation : chez moi
Date d'inscription : 15/04/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mar 7 Nov 2006 - 6:12 Mar 7 Nov 2006 - 6:12 | |
| Ce qui moi m'étonne, c'est que sur les liens que j'ai donné, la mesure ne se fait pas sur le déplacement horizontal, mais vertical. J'avoue ne rien avoir trouvé sur un déplacement horizontal. | |
|   | | Lepigeon
Modérateur



 
Nombre de messages : 3010
Age : 47
Localisation : Montréal et ailleurs
Date d'inscription : 27/10/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mar 7 Nov 2006 - 8:15 Mar 7 Nov 2006 - 8:15 | |
| - David a écrit:
- Ce qui moi m'étonne, c'est que sur les liens que j'ai donné, la mesure ne se fait pas sur le déplacement horizontal, mais vertical. J'avoue ne rien avoir trouvé sur un déplacement horizontal.
Je ne me suis pas amusé à reprendre les formules, mais déplacement vertical ou horizontal, ce n'est pas le plus important, car l'un peut se déduire de l'autre vu que la longueur de la ficelle est fixe. | |
|   | | Lepigeon
Modérateur



 
Nombre de messages : 3010
Age : 47
Localisation : Montréal et ailleurs
Date d'inscription : 27/10/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mar 7 Nov 2006 - 8:28 Mar 7 Nov 2006 - 8:28 | |
| - marceau a écrit:
- salut
bravo a pierre pour ce sujet passionnant
je me pose une question:
est-ce que la dureté de la "cible" (pate a modeler + sable) n'intervient pas dans le calcul ?, sur une cible plus "dur" l'energie serait retransmise instantanément, alors que dans du sable elle est absorbée et ne permet pas au pendule de parcourrir la meme distance , ce qui expliquerait une vitesse légerement pessimiste ?
 Je ne suis pas certain de ce que tu avances. L'énergie du plomb n'est que faiblement retransmise: le plomb se déplace avec le pendule. Il doit y avoir des variations suivant la surface, mais les facteurs sont multiples, en particulier pour les pertes par frottement. Le temps de la collision est certes plus long si la pénétration est plus grande, et l'ensemble commence à se déplacer avant que le plomb cesse de se déplacer par rapport au pendule, de sorte que la vitesse n'est pas intégralement transmise horizontalement, mais ce temps est-il significatif? Un beau petit problème à creuser en tout cas  http://ici.cegep-ste-foy.qc.ca/profs/rfoy/capsules/pendule.html | |
|   | | Pierre
Intermédiaire



 
Nombre de messages : 97
Age : 78
Localisation : Toulouse
Date d'inscription : 04/04/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mar 7 Nov 2006 - 9:14 Mar 7 Nov 2006 - 9:14 | |
| Réponse à David, fbastin et Marceau :
- Déplacement horizontal ou vertical : c'est vrai que les sites sur le pendule balistique donnent en général des formules de calcul à partir du déplacement vertical du pendule. C'est parceque ces sites sont faits par des profs de physique qui s'intéressent avant tout à la théorie mécanique et à des exercices d'école pour leurs élèves. En fait le déplacement horizontal et le déplacement vertical sont liés, car le point bas de la ficelle décrit un cercle autour du point d'accrochage sous plafond. La formule qui lie les deux est :
(Dv) = (Dh)² / 2L , où Dv est le déplacement vertical, Dh le déplacement horiontal, et L la longueur de la ficelle, le tout dans les même unités (mm ou m). Cette formule est valable pour des faibles déplacements (Dv faible devant L), ce qui est le cas dans notre pendule.
Comme la mesure du déplacement horizontal est beaucoup plus facile et plus précise que celle du déplacement horizontal vertical, j'ai transformé les formules données dans les sites en introduisant le déplacement horizontal.
Certains sites font aussi intervenir dans le calcul la période d'oscillation du pendule en seconde. En fait, la période est liée aussi à la longueur de la ficelle, donc il y a des équivalences entre les différentes formules. Celle que je donne dans mon post me parait la plus commode quand on veut faire des vraies mesures, et pas seulement de la théorie. Pour les physiciens, je précise que le pendule balistique tel que décrit dans mes schémas diffère sensiblement du "pendule simple" d'école : il y a deux ficelles, et des articulations implicites au niveau des points de suspension : le corps du pendule se translate sans rotation contrairement au cas d'un pendule simple : il faut donc utiliser les formules avec prudence.
- Frottement du plomb dans la pâte à modeler et dans le sable : là, je suis un peu moins sûr de moi... c'est vrai que le mouvement du pendule démarre avant que le plomb ne soit complêtement arrêté par le sable, mais il me semble que celà ne doit pas influencer beaucoup le déplacement final du pendule car le temps d'arrêt du plomb (qq centièmes de seconde) est très court par rapport à la période d'oscillation du pendule (environ 1 seconde).
Je m'arrête là, car ce forum ne doit pas devenir un cours de physique : il faut garder un peu de temps pour tirer à la carabine, quand même !!
Pierre
Dernière édition par le Ven 11 Mai 2007 - 8:23, édité 2 fois | |
|   | | Admin
Pilier



 
Nombre de messages : 32648
Age : 47
Localisation : chez moi
Date d'inscription : 15/04/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mar 7 Nov 2006 - 9:22 Mar 7 Nov 2006 - 9:22 | |
| Au contraire, même si nous ne sommes pas sur un forum de physique, tous ces calculs et théories mathématiques me passionnent et je ne dois pas être le seul ! | |
|   | | Shura
Parrain



 
Nombre de messages : 23376
Age : 47
Localisation : Grove street, Los Santos
Date d'inscription : 30/08/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mar 7 Nov 2006 - 10:06 Mar 7 Nov 2006 - 10:06 | |
| - David a écrit:
- Au contraire, même si nous ne sommes pas sur un forum de physique, tous ces calculs et théories mathématiques me passionnent et je ne dois pas être le seul !
+1 ! Les sciences ... elles me manquent  , j'aurais jamais du les abandonner ... Je suis donc très intéressé par l'aspect mathématique du tir, la balistique, ... Donc continuons, continuez c'est très intéressant ...  _________________ "A quelle heure Oxford arrive-t-il à ce train ?" Albert Einstein  | |
|   | | Pierre
Intermédiaire



 
Nombre de messages : 97
Age : 78
Localisation : Toulouse
Date d'inscription : 04/04/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mar 7 Nov 2006 - 10:33 Mar 7 Nov 2006 - 10:33 | |
| - David a écrit:
- Au contraire, même si nous ne sommes pas sur un forum de physique, tous ces calculs et théories mathématiques me passionnent et je ne dois pas être le seul !
Message reçu. ça me plait aussi, donc plus d'auto-censure sur la physique et les mathématique des armes AC ! Cordialement, Pierre | |
|   | | Invité
Invité

 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Dim 6 Mai 2007 - 8:30 Dim 6 Mai 2007 - 8:30 | |
| Salut tout le monde
la mesure de l'energie avec laquelle une carabine à air propulse un plomb sans disposer d'appareillage sophistiqué m'interesse beaucoup . J'y ai beaucoup pensée . Je crois avoir parvenu à des techniques personelles que je discuterais avec vous plus tard si cela vous interesse .
L'idée du pendule pour mesurer la vitesse du plomb est bonne mais je crois qu'il ya un detail auquel Pierre n'a pas fait attention .
le principe de la "technique du pendule" si je peux l'appeler ainsi c'est de transferer l'energie cinétique du plomb au pondule . l'etude du pendule et de ses ossilations permet facilement la mesure de l'energie transmise sous forme de mouvement . le problème parrait résolu . Mais la question que moi je me pose c'est : est ce que toute l'energie cinétique du plomb est transformée en mouvement du pendule ? moi personellemet je crois que c'est non : une partie de l'energie cinetique du plomb est transmise effectivement sous forme de mouvement (ossilations) mesurable, une autre partie d'energie est absorbée par la pate à modeler : pour creuser un trou sur la pate à modeler le plomb perd de l'energie . et je pense que plus la masse du pendule est importante plus l'energie absorbéé par la pate a modeler est importante .
A mon avis la "technique du pendule" n'est pas fiable pour mesurer la vitesse du plomb . Merci comme meme pour l'effort fourni et pour le partage de l'information . |
|   | | Didier
Habitué Des Lieux


Nombre de messages : 326
Localisation : France Blois (41)
Date d'inscription : 31/05/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Dim 6 Mai 2007 - 17:51 Dim 6 Mai 2007 - 17:51 | |
| - khalid a écrit:
A mon avis la "technique du pendule" n'est pas fiable pour mesurer la vitesse du plomb . Merci comme meme pour l'effort fourni et pour le partage de l'information . Je trouve ce sujet bien intéressant moi aussi... Je suis assez d'accord avec Khalid... Il serait assez intérressant de modifier la nature de la matière pour évaluer la dispersion des mesures... Pête à modelée neuve et molle... Bloc de savon plus dur... Argile à modeler... pour voir ce que cela donne sur un même montage... | |
|   | | Pierre
Intermédiaire



 
Nombre de messages : 97
Age : 78
Localisation : Toulouse
Date d'inscription : 04/04/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Dim 6 Mai 2007 - 20:13 Dim 6 Mai 2007 - 20:13 | |
| - khalid a écrit:
- est-ce que toute l'energie cinétique du plomb est transformée en mouvement du pendule ? moi personellemet je crois que c'est non : une partie de l'energie cinetique du plomb est transmise effectivement sous forme de mouvement (ossilations) mesurable, une autre partie d'energie est absorbée par la pate à modeler : pour creuser un trou sur la pate à modeler le plomb perd de l'energie . et je pense que plus la masse du pendule est importante plus l'energie absorbéé par la pate a modeler est importante .
A mon avis la "technique du pendule" n'est pas fiable pour mesurer la vitesse du plomb . Merci comme meme pour l'effort fourni et pour le partage de l'information . Kahlid, tu as partiellement raison sur la perte d'énergie, mais tu te trompes quant à la conclusion que tu en tires : Ce que tu n'as pas bien vu, c'est que le principe de la mesure est basé sur la conservation de la quantité de mouvement "mv", qu'il ne faut pas confondre avec l'énergie cinétique. L'énergie cinétique ne se conserve pas dans le cas d'un choc non élastique. (L'énergie totale se conserve cependant : energie cinétique du plomb = energie de déformation + energie cinétique du pendule) Le pendule balistique est une méthode tout à fait fiable pour mesurer la vitesse d'un projectile. Il a été inventé au 18eme siècle par un mathématicien-physicien à une époque où il n'existait pas de chronographe à cellule photo-électrique et il a été utilisé par des générations d'ingénieurs en armement et d'officiers artilleurs polytechniciens... J'avoue que je me suis posé moi aussi la question de l'énergie dissipée dans la pâte à modeler et dans le sable placé dans le pendule. Comme je n'étais pas tout à fait clair, j'ai ressorti mes vieux bouquins de mécanique aux chapitres "chocs et percussions entre solides", "quantité de mouvement", et "énergie cinétique". Voici ce qu'il faut retenir (c'est un peu long désolé, mais il faut bien entrer dans les détails si on veut démontrer les choses rigoureusement 1) Dans la théorie des chocs entre deux solides, il faut distinguer : - les chocs parfaitement élastiques (une corps rebondit sur l'autre) - les chocs parfaitement inélastiques ou "chocs mous", dans lesquels les deux corps fusionnent en se déformant, et ont la même vitesse à l'issue du choc. C'est le cas du pendule balistique. - les cas intermédiaires (partiellement élastiques). 2) quelque soit le type de choc, il y a une grandeur physique qui se conserve pendant le choc : c'est la "quantité de mouvement" m.v. (à ne pas confondre avec l'énergie cinétique) : soit 2 corps de masses m1 et m2, v1 et v2 leurs vitesses avant le choc et v'1 et v'2 les vitesses après le choc. Les vitesses sont ici des vecteurs. La quantité de mouvement avant le choc est : m1 v1 + m2 v2' La quantité de mouvement après le choc est : m1 v'1 + m2 v'2 ces deux quantités sont égales : m1 v1 + m2 v2 = m1 v'1 + m2 v'2 et ceci est toujours vrai, que le choc soit élastique ou mou. Dans le cas du pendule balistique avec du sable et de la pâte à modeler, il s'agit d'un choc parfaitement mou : le plomb est entièrement arrêté par le pendule, et il a ensuite la même vitesse que le pendule. Soit m1 est la masse du plomb, m2 celle du pendule, et v1 la vitesse du plomb avant le choc (v2=0 car le pendule est immobile avant le choc). La quantité de mouvement avant le choc est alors : m1 v1. après le choc, la vitesse du pendule (et du plomb) est v'2. La quantité de mouvement après le choc est donc : (m1+m2) v'2. et la conservation s'écrit : m1 v1 = (m1+m2) v'2. la vitesse du pendule est donc V'2 = m1 v1 / (m1+m2) Comme la masse du plomb est très petite devant celle du pendule, la parenthèse (m1+m2) est quasiment égale à m2. on peut donc simplifier la formule finale qui lie la vitesse du plomb à la vitesse du pendule : v'2 = (m1/m2) v1 on voit donc que l'on peut déduire v1 si on mesure la vitesse du pendule v'2. En fait on ne mesure pas directement v'2, mais on la déduit à partir de l'amplitude du mouvement d'oscillation du pendule. Donc la mesure de la vitesse d'un projectile au pendule balistique est correcte. il n'est pas question d'énergie dans ce calcul. 3) On n'a pas encore parlé d'énergie cinétique dans ces calculs. Essayons de calculer maintenant les énergies cinétiques avant et après le choc et voyons si elles sont égales : - énergie avant le choc (celle du plomb) : E = (1/2) m v1² - énergie après le choc (celle du pendule + plomb ) : E' = (1/2) (m1+m2) v'2² ou encore, en négligeant la masse du plomb devant celle du pendule : E' = (1/2) m2 v'2² on remplace ensuite v'2 par sa valeur donnée plus haut : E' = (1/2) m2 [(m1/m2) v1]² soit : E' = (1/2) m2 (m1²/m2²) v1² ou encore : E' = (1/2) m1 v1² m1/m2. or la première partie de l'expression(1/2) m1 v1² n'est autre que l'énérgie avant le choc E. Donc : E' = E m1/m2 En conclusion, on voit que l'énergie cinétique après le choc n'est pas égale à l'énergie cinétique avant le choc : elle est plus faible d'un facteur m1/m2. Elle est en fait baucoup plus faible puisque m1 est petit devant m2. Finalement, la quantité de mouvement se conserve, mais pas l'énergie cinétique. Mais alors, où est passé l'énergie perdue ? eh bien c'est justement l'énergie qui sert à déformer la pate à modeler pendant le choc. Cette énergie est finalement dissipée sous forme de chaleur. Résumons nous :-la quantité de mouvement se conserve, et c'est ça que l'on utilise dans la mesure, qui est parfaitement fiable. - l'énergie cinétique du plomb n'est pas entièrement transformée en energie cinétique du pendule : la plus grande partie est dissipée par la déformation de la pate à modeler et du sable (Kahlid a raison sur ce point). - en fait l'énergie se conserve, à condition de parler d'énergie totale : énergie cinétique du plomb = energie cinétique du pendule + energie de déformation de la pate à modeler. remarque : il ya un cas ou l'énergie cinétique se conserve aussi : c'est dans le cas d'un choc parfaitement élastique, où les corps ne sont pas déformés après le choc. Ce cas n'est pas un cas réaliste pour un corps en plomb, car le plomb est plutot mou. Voila ! Amicalement Pierre | |
|   | | Didier
Habitué Des Lieux


Nombre de messages : 326
Localisation : France Blois (41)
Date d'inscription : 31/05/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Lun 7 Mai 2007 - 14:57 Lun 7 Mai 2007 - 14:57 | |
| Je te suis kalid (je voulais dire Pierre...) mais j'ajoute cependant une reserve... La quantité de mouvement n'est pas toujours conservée lors d'un choc... En effet pour un systeme mécanique quelconque considéré comme ici avec des points d'encrage au plafond la variation du torseur cinétique lors d'un choc (vecteur quantité de mouvement et moment cinétique) n'est pas toujours nulle... "La variation du torseur cinétique est égale au torseur des percussions extérieurs" Et dans le cas du pendule que tu as décrit il faut s'assurer que les percussions de réaction au niveau des ficelles restent nulles.. Sinon il n'y a pas non plus de conservation de la quantité de mouvement... A priori (il faut que je pose ça sur le papier) Pour que les percusions de réaction soient effectivement nulles il faut que le tir soit bien horizontal et parfaitement dans l'axe du centre de gravité... Si le tir à lieu un peu au dessus ou un peu au dessous de l'axe ou si le tir est légérement descendant alors les ficelles imposeront une réaction (percussion de réaction) dont l'intensité (en N.s) est du même ordre que la percussion du projectile et qui ne peuvent donc pas être négligé... Il faudrait que je mette au propre la résolution de ce probleme de méca et que je le scanne pour mettre ça au clair dans ma tête ... Et puis voir surtout si ça perturbe vraiment beaucoup... Oh là là ça fait longtemps que j'ai pas traité ce genre d'exercice !!
J'ajoute que parmi les hypothèses classiquement adoptées figure l'hypothèse que la durée du choc est "infiniment" petite... de sorte que la position relative des solides peut être supposée constante lors du choc... L'hypothèse est d'autant mieux validée que la matière choisi stope brutalement le projectile (l'important est qu'il reste captif)... C'est pourquoi je serais curieux quand même de voir les écarts de mesure induite par une modification de texture de la pâte... Bon ici le rapport des masses est tel que bof... Peu d'effet je crois...
Dernière édition par le Lun 7 Mai 2007 - 16:44, édité 1 fois | |
|   | | Pierre
Intermédiaire



 
Nombre de messages : 97
Age : 78
Localisation : Toulouse
Date d'inscription : 04/04/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Lun 7 Mai 2007 - 15:53 Lun 7 Mai 2007 - 15:53 | |
| C'est vrai, Didier, il faut que les reactions de percussion des ficelles soient nulles pour que la quantité de mouvement se conserve bien. Merci d'avoir précisé ce point que je n'avais pas entièrement compris ni formalisé dans mon post.
Comme mon pendule est à symétrie cylindrique, la condition sera respectée si la trajectoire du plomb est bien confondue avec l'axe du cylindre. C'est ce que j'ai intuitivement recherché en réglant le montage.
Au début, je ne tirais pas tout à fait dans l'axe et on voyait effectivement une oscillation de rotation se superposer à l'oscillation linéaire du pendule. Dans ce cas la mesure donne une vitesse de plomb plus faible que la valeur vraie. Il n'est pas très difficile de soigner le réglage.
Concernant la durée du choc : à vue de nez et à l'oreille, je dirais que le plomb s'arrête en moins de 0.1 seconde. Ce n'est pas infiniment court mais c'est quand même petit devant la periode d'oscillation du pendule qui est de l'ordre de 2 secondes dans mon montage. On peut donc considérer que le pendule n'a pas encore beaucoup bougé quand le plomb a fini sa course d'arret. C'est ça qui est important non ?
Je persiste à croire que le pendule balistique (bien utilisé) permet de mesurer la vitesse d'un plomb d'arme AC avec une précision acceptable (disons +/- 15%). Bien sûr, on n'atteindra pas la précision d'un chronographe moderne ; l'intérêt du pendule est surtout historique...
Pierre. | |
|   | | Didier
Habitué Des Lieux


Nombre de messages : 326
Localisation : France Blois (41)
Date d'inscription : 31/05/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Lun 7 Mai 2007 - 16:50 Lun 7 Mai 2007 - 16:50 | |
| - Pierre a écrit:
- Comme mon pendule est à symétrie cylindrique, la condition sera respectée si la trajectoire du plomb est bien confondue avec l'axe du cylindre. C'est ce que j'ai intuitivement recherché en réglant le montage.
...
Je persiste à croire que le pendule balistique (bien utilisé) permet de mesurer la vitesse d'un plomb d'arme AC avec une précision acceptable (disons +/- 15%). Bien sûr, on n'atteindra pas la précision d'un chronographe moderne ; l'intérêt du pendule est surtout historique...
Pierre. Je viens de poser ça laborieusement sur le papier et effectivement je partage maintenant entièrement ton avis... Je recherchais quels facteurs pouvaient bien poser probleme dans les mesures faites par Loulator... Et je ne vois pas ce qui peut conduire à un tel écart... | |
|   | | Invité
Invité

 |  Sujet: reponse a pierre . Sujet: reponse a pierre .  Mer 9 Mai 2007 - 9:08 Mer 9 Mai 2007 - 9:08 | |
| Tout d'abord je tiens à vous préciser que c'est avec avec mes bagages scientifiques de la classe terminale (s'il en reste encore) que je raisonne. D'ailleurs les études que j'ai effectuées après le bac n'ont rien à avoir avec la physique et les mathématiques. Je dis cela pour encourager les autres membres du forum à participer à cette discussion.
Pierre , le fait d'accepter qu'il y'a perte de l'énergie cinétique du plomb au dépend de la déformation de la pâte (trou creusé sur la pâte après le choc) devrait normalement te suffire pour être d'accord avec moi .
Dans ton expérience et pour pouvoir estimer la vitesse du plomb , sans le dire directement , tu as supposé que l'énergie cinétique du plomb est égale à l'énergie mécanique transmise au pendule et tu n'as pas pris en considération l'énergie responsable de la déformation de la pâte (trou creusé sur la pâte).
Tu demandes de ne pas confondre énergie cinétique et quantité de mouvement. Moi je ne les confonds pas mais je pense qu'elles sont étroitement liées :
EC (énergie cinétique) = 1/2 mv2
QM (quantité de mouvement) = mv
Qu'on raisonne avec l'énergie cinétique ou la quantité de mouvement normalement on devrait aboutir aux mêmes résultas
Dans ton raisonnement tu penses qu'il y'a perte de l'énergie cinétique et qu'il y'a en même temps conservation de la quantité de mouvement. C'est faux :
S'il y'a perte de l'énergie cinétique après un choc il y'a forcément perte de la quantité de mouvement aussi.
Pour qu'il ait conservation de la quantité de mouvement avant et après un choc il faut que les deux corps ne soient pas déformables. Tu t'es donc trompé : il n'a y'a pas de conservation de la quantité de mouvement dans ton expérience et l'équation v'=( m1 / m2 ) v n'est pas valable .
Je te donne un contre exemple :
Une voiture de masse m1 roule à une vitesse v1 = 80 km/h (22,2 m/s) et s'ecrase contre une montagne de masse m2 . Apres le choc la voiture reste collée à la montagne.
QM avant le choc = m1 v1 + m2 v2
v2 = 0 -------------------) QM avant choc = m1 v1
QM après le choc = ( m1 + m2 ) v'
v' = vitesse de la voiture et de la montagne après le choc . v' = 0
-----------------) QM après choc = 0
Il n'a pas de conservation de la quantité de mouvement dans cet exemple : l'énergie cinétique et la quantité du mouvement de la voiture avant le choc sont perdues après le choc en entraînant l'écrasement et la déformation de la voiture.
Conclusion :
La vitesse du plomb mesurée par la technique du pendule balistique de Pierre est inférieure à la vitesse réelle du plomb. Cette technique n'est pas donc fiable pour mesurer la vitesse avec laquelle une carabine à air propulse un plomb.
Attention cela ne veut pas dire que le pendule balistique ne sert à rien . Pas du tout. Je pense que le mathématicien physicien qui a inventé cette technique a bien fait attention à l'énergie absorbée par le sable (pâte à modeler dans notre cas) mais j'ai deux suppositions :
- peut être que le mathematicien-physicien ne cherchait pas à calculer la vitesse réelle du projectile lancé par une arme à feu. Il cherchait peut être un moyen pour comparer la puissance des armes .
- ou peut être que dans le cas d'une arme à feu l'énergie absorbée par le sable est négligeable devant l'énergie mécanique transmise au pendule balistique.
Pour finir, je crois avoir une idée pour que l'on puisse mesurer la vitesse du plomb tout en utilisant le principe du pendule balistique : des modifications sur le pendule de Pierre . Mais je ne vous en parlerais que une fois monsieur Pierre retrouve la raison et affirme que mon raisonnement est correct. |
|   | | Pierre
Intermédiaire



 
Nombre de messages : 97
Age : 78
Localisation : Toulouse
Date d'inscription : 04/04/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mer 9 Mai 2007 - 14:01 Mer 9 Mai 2007 - 14:01 | |
| Kahlid,
si tu t'es senti attaqué par mon post, ce n'était pas du tout mon intention et j'en suis désolé. Je suis d'accord avec certains de tes arguments, qui m'ont d'ailleurs amené réfléchir et mieux comprendre certains points de la théorie. Mais il y a d'autres points sur lesquel je ne te suis pas, et donc c'est normal de discuter. Je crois être resté toujours correct, en essayant d'argumenter et en restant toujours au niveau des idées.
Le pendule ballistique n'est ni mon invention ni ma propriété, et je ne me sentirai pas du tout vexé si quelqu'un démontre que la théorie est fausse, que ça ne vaut rien, et que tous les gens qui ont mis au point cette théorie et qui l'ont utilisée pendant des années n'avaient rien compris. Mais pour l'instant, je reste sur mes positions (partagées aussi par Didier, si j'ai bien compris) :
a) tu as raison quand tu dis que l'énergie cinétique du plomb n'est pas entièrement transformée en énergie cinétique du pendule : une partie de l'énergie du plomb sert à creuser le trou dans la pâte et dans le sable. Nous sommes bien d'accord sur ce point. Il n'y a donc pas de conservation de l'énergie cinétique dans un choc mou.
b) il y a conservation de l'énergie totale (c'est une loi universelle):
- énergie totale avant le choc = énergie cinétique du plomb
- énergie totale après le choc = énergie cinétique de l'ensemble pendule/plomb + énergie de déformation du pendule (de la pâte).
La déformation de la matière produit un dégagement de chaleur qui se dissipe ensuite dans la nature. L'équivalence est 1 calorie = 4.18 joules.
c) il y a conservation de la quantité de mouvement, même dans le cas d'un choc mou, pourvu que le temps de déformation soit petit (c'est à dire que le pendule ne bouge quasiment pas pendant l'arret du plomb).
On pourrait d'ailleurs remplacer la pate à modeler et le sable par un bloc d'acier dur sur le quel le plomb viendrait s'écraser en de déformant et en s'échauffant. La quantité de mouvement se conserverait dela même manière , la vitesse du pendule étant toujours v'=v1 (m1/m2) pourvu que le plomb ne rebondisse pas en dehors du pendule.
d) Tu dis : "S'il y'a perte de l'énergie cinétique après un choc il y'a forcément perte de la quantité de mouvement aussi" : eh bien non, il n'y a pas de loi physique qui dise cela. La quantité de mouvement n'est pas équivalente à une énergie, et ne s'exprime pas dans la même unité. Deux objets peuvent d'ailleurs avoir la même quantité de mouvement et des énergies cinétiques différentes :
exemple : un objet A de masse 1 kg et de vitesse 10m/s a une QM de 10 kgxm/s et une énergie cinétique de 50 Joule. Un autre objet B de masse 0.1 kg et de vitesse 100m/s a aussi une QM de 10 kgxm/s mais une énergie cinétique de 500 joules.
e) Ton exemple de la voiture qui s'écrase sur une montagne est discutable. La montagne est ici un objet mal défini : quelle est sa masse, quells sont ses limites en profondeur, comment est-elle ancrée dans le sol ?(comment est elle fixée au reste de la planète )? Si on condidère que la montagne est un immense corps solide flotant sur le magma profond, alors l'impulsion fournie par la voiture va se transmettre à la montagne et entrainer un petit déplacement (qui va contribuer à la dérive des continents !). La vitesse de déplacement sera certes très faible, mais il y aura quand-même conservation de la quantité de mouvement. La vitesse diminuera ensuite à cause de la viscosité du magma. Si tu considère au contraire que la montagne est rigidement fixée au reste de la planète, alors c'est à la Terre entière que la quantité de mouvement est transférée. Son mouvement de rotation va être légèrement perturbé (mais la Terre aura subi une perturbation opposée quand la voiture a accéléré pour se lancer sur la montagne : le bilan sera nul, ouf!)
Tu vois que ce n'est peut-être pas aussi évident que tu le penses.
Ceci dit, je serai heureux de poursuivre la discussion si tu le souhaites, et aussi de connaitre tes idées pour améliorer le système, ou sur d'autres méthodes de mesure vitesse. Voici par exemple un site qui décrit brievement quelques méthodes, dont le pendule balistique.
http://www.fftir.asso.fr/index.php?FicheNum=74
Cordialement,
Pierre | |
|   | | Didier
Habitué Des Lieux


Nombre de messages : 326
Localisation : France Blois (41)
Date d'inscription : 31/05/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mer 9 Mai 2007 - 16:26 Mer 9 Mai 2007 - 16:26 | |
| Salut Khalid, J'ai lu ton post avec attention et ton raisonnement montre que dans une certaine mesure tu fais preuve de bon sens et d'un redoutable esprit critique... Mais hélas les lois de la physique échapent parfois au bon sens commun... Je voudrais venir en aide au raisonnement de Pierre qui est conforme à tout ce que l'on peut lire dans les ouvrages spécialisés et traitant de la mécanique du choc... Pour info il y a par exemple les cours en ligne de l'école d'ingénieur INSA lyon et des centaines d'autres sites... Et j'ai sur mon bureau 4 collections d'ouvrages de sciences physiques qui disent la même chose... Bon Pierre à tout dit... L'énergie cinétique ne se conserve pas lors d'un choc... Et le phénomène de défomation du projectile n'est pas du tout ignoré dans son raisonement... La technique de résolution permet même de calculer cette perte systematique d'énergie cinétique... C'est bien la quantité de mouvement qui est conservée lors du choc... Tiens j'ai ici un autre bouquin de mécanique destiné à des élèves de Bac ou BTS sections industrielles... Il y a justement un exo avec le pendule où figure seulement les réponses... Le temps de scanner et je le joint à ce post... On y voit que non seulement les pertes occasionnées par la déformation du projectile ne sont pas ignorée mais quelles representent pour cet exemple 99.8% de l'energie cinétique initiale... 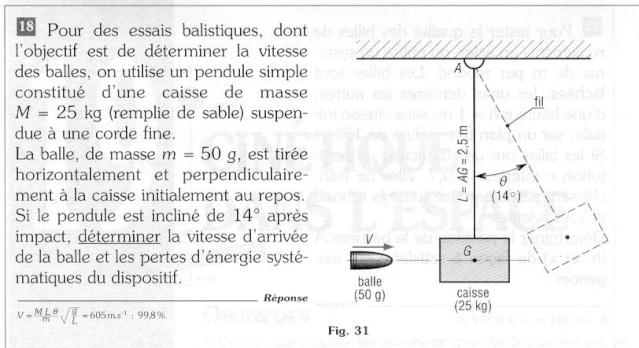 | |
|   | | Invité
Invité

 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Mer 9 Mai 2007 - 19:45 Mer 9 Mai 2007 - 19:45 | |
| Salut Didier , j'aurais aimé que tu sois de mon coté . ce n'est pas grave .
Salut Pierre
au contraire Pierre ça me fait très plaisir de discuter avec toi . Je ne fais que défendre mes opinions .
quand je dis qu'il n'y’a pas de conservation de la quantité de mouvement je parle de la quantité de mouvement mesurable QM = mv . cela exclue la quantité de mouvement responsable de déformation.
Je ne parle pas donc de la quantité de mouvement globale .
Si non moi aussi je vous dirais qu'il n'y’a pas de perte de l'énergie cinétique puis ce que finalement rien ne se perd tout se transforme !
Pierre je te pose une question : Pourquoi tu n'as pas respecté la loi de la conservation de la quantité de mouvement globale pour arriver à l'équation v' = m1 v1 / (m1+m2) v
tu aurais du raisonner ainsi :
QM avant choc = QM du plomb +QM du pendule
= m1v1 + 0
= m1v1
QM après choc = QM du pendule + QM responsable de deformation de pate
QM avant choc = QM après choc ---------)
m1 v1 = (m1+m2) v’+ QM responsable de déformation de pate
---------) v’= (m1v1 – QM responsable de deformation)/ (m1+m2)
en analysant cette équation on remarque que :
v’ varie selon qu’il y’a ou pas déformation .
S’il n’y’avait pas déformation dans ton expérience le pendule bougerait plus . et la valeur de la vitesse du plomb avant le choc mesurée par ton pendule serait plus élevée que celle que tu as réellement trouvée .
Plus la déformation est importante moins est la valeur de v’ ( cela veut dire que plus la pate à modeler est deformée moins bougerait le pendule de pierre après le choc)
Dans ton raisonnement tu as supposé que QM responsable de la déformation de la pate à modeler est égale à 0 . tu as donc supposé que le plomb et le pendule dont la pate à modeler fait parti ne sont pas déformables . et cela n’est pas vrais : la pate à modeler est bien deformée après le choc !
Dans ton experience tu n’a pas mesurer la quantité de mouvement ayant servi à la déformation de la pate à modeler . Tu as calculé uniquement la quantité de mouvement du pendule .
Je te donne un exemple :
quand une boule de billard butte contre une autre boule de billard il y’a conservation de la quantité de mouvement ( QM = m v ) apres le choc qu’on peut mesurer . et cela parce que les boules de billard sont fermes et ne sont pas déformables .
Si on remplace les boules de billard par des boules en pate à modeler , après le choc ces boules bougeraient mois que dans la première expérience .il y’a perte de la quantité de mouvement (QM = m v).
Là aussi je parle de la quantité de mouvement QM = m v . et je ne parle pas de la quantité de mouvement globale .
imaginez qu’on joue au billard avec des boules en pate à modeler ! il y’a conservation de la quantité de mouvement globale mais je ne pense pas qu’on peut jouer avec .
dans l’expérience 2 il y’a conservation de la quantité de mouvement globale mais il n’y’a pas de moyen pour mesurer les quantité de mouvement responsable des déformations .
l’équation v’= m1v1 / (m1+m2) n’est pas valable dans l’expérience avec les boules en pate à modeler car il y’a déformation des deux boules après le choc et la QM de mouvement responsable des déformations devrait figurer dans l’équation .
v’= ( m1v1 – QM responsable des déformation )/ (m1+m2)
s'il te plait Pierre essaie de me comprendre parce que je pense avoir raison . |
|   | | Didier
Habitué Des Lieux


Nombre de messages : 326
Localisation : France Blois (41)
Date d'inscription : 31/05/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Jeu 10 Mai 2007 - 5:32 Jeu 10 Mai 2007 - 5:32 | |
| Pour ceux qui ne lisent pas tout et qui désirent aller à l'essentiel... Je réedite ce post pour bien montrer qu'à l'issue de la causerie il ressort que les équations que donne Pierre sont valides !
----------
Salut à tout les passionnés du pendule...
Je viens de refaire l'exo du pendule à deux fils... La dernière fois je me suis trompé dans ma résolution... Je pense comprendre maintenant pourquoi Loulator obtient un résultat aussi éloigné de la réalité... c'est parce que l'on ne doit pas faire usage d'un tel pendule ! (avec deux fils) Il faut en revenir au pendule simple (à un fil ) ou pendule solide articulé sur un axe... Voir par exemple ici pour le calcul...
http://fred.elie.free.fr/pendule_balistique.htm
Ensuite il faut revenir à la théorie de la mécanique des chocs... En effet il ne faut surtout pas partir du postula qu'il y a toujours conservation de la quantité de mouvement... (mais pas pour les raisons que pose Khalid... voir deuxieme partie de ce post) En effet pour traiter un tel problème la première chose à écrire c'est que pour le systeme mécanique considéré (ici je choisi comme systeme le pendule seul) :
1) la variation du vecteur quantité de mouvement au cours du choc = somme des "vecteurs percussions" (ici il y a trois vecteurs percussion: celui du au projectile et les deux "percussions de réaction" au niveau des point de fixation !!! et non sauf configuration très particulière... Ils ne sont pas nul même pour un tir honrizontal passant par le centre de gravité !!)
2) la variation du vecteur moment cinétique (calculé en un point quelconque) au cours du choc = somme des vecteurs "moment de percussion" appliqués au pendule (ici 3... les moments des 3 vecteurs percussions)
Et ici rien à faire ! Je ne parviens pas à trouver une astuce dans les équations pour annuler ces percussions de réaction... Il n'y a pas pour ce cas conservation de la quantité de mouvement... Mais pas pour les raisons que tu invoque Khalid...
Ca c'est le deuxieme volet de ma remarque...
Khalid... La théorie des chocs n'oublie pas du tout de prendre en compte la déformation localisée des pièces qui viennent se heurter... La déformation du profectile qui vient s'écrabouillé n'est pas oubliée... Cet aspect est pris en compte au travers de l'équation complémentaire dite "équation de restitution" On utilise toujour ce fameux "coeficient de restitution" "e" de l'énergie cinétique... Qui peut varier entre 0 et 1. e=1 c'est un choc elastique soit aucune déformation residuelle (cas de tes boules de billard) e=0 c'est un choc mou... C'est le cas dans le cadre de la résolution du pendule... Pierre ne l'a pas oubliée... Le plomb après le choc reste accroché au pendule c'est ce qui le conduit à écrire (m+M) "les deux solides n'en forme plus qu'un ! pas de vitesse de séparation...
Kalid une autre approche pour tenter de te convaincre du bien fondé de cette approche c'est de te dire que si tu considère en effet l'évolution du système mécanique constitué des deux protagonistes (pendule + balle) et bien en effet on peut ne rien savoir sur la compléxité des efforts exercés entre les deux lors du choc et des déformations occasionnées car aussi complexe soient-ils se sont des efforts intérieur au systeme considéré et en vertu du principe des actions-réaction (3ème loi de Newton) cette termes de percusions intérieures s'annulent mutuellement...
Enfin pour conclure sur ce pendule à deux fils j'aimerais bien quand même que tu me confirme Pierre qu'il y à bien un probleme liés à ces percussions de réaction...
Si tu trouve le temps peux tu faire avec ton pendule une série de mesures (même type de plomb même carabine bien sûr ) mais en faisant varier de façon significative soit la longueur des fils tout le reste etant maintenu identique soit en faisant varier seulement la masse du pendule en y collant des masses réparties symétriquement... Je pense que ta formule te conduira à des résultats très différents... Car d'après les relations que j'obtiens cette formule est obtenue en traitant le probleme comme si il n'y avait aucun effort de réaction sur les fils... Et cette situation ne se produit que si l'on a miraculeusement un rapport particulier entre m et M et v et V... pour être précis seulement si (m+M).V=m.v où v est la vitesse du plomb et V la vitesse horizontale communiquée au pendule... Et je pense que par le plus grand des hasard tu te trouve dans un cas assez proche de cette situation et pas Loulator...
Enfin pour finir un lien pour ceux que les équations ne font pas fuir... Voici en lien un cour au format PDF sur la mécanique des chocs...
http://docinsa.insa-lyon.fr/polycop/download.php?id=104733&id2=1
Merci à tout les deux de m'avoir obligé à me replonger dans un chapitre que je n'avais pas revisité depuis bien longtemps...[i]
Dernière édition par le Ven 11 Mai 2007 - 16:17, édité 2 fois | |
|   | | Pierre
Intermédiaire



 
Nombre de messages : 97
Age : 78
Localisation : Toulouse
Date d'inscription : 04/04/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Jeu 10 Mai 2007 - 12:21 Jeu 10 Mai 2007 - 12:21 | |
| Didier,
Merci pour ce post très riche! Je crois comprendre ce que tu me dis, mais je commence à atteindre mes limites : j'étais ingénieur, mais en optique, et mes souvenirs de mécanique de math-sup/math-spé sont déjà bien loin....
Je vais donc prendre le temps de réfléchir au bilan des percussions dans le cas du pendule à 2 fils, et je te répondrai dès que j'aurai les idées claires.
Kahlid, je te répondrai aussi.
PS (EDIT) : Didier, en relisant la fin de ton post, je m'interroge sur le sens de ta phrase : "Et cette situation ne se produit que si l'on a miraculeusement un rapport particulier entre m et M et v et V... pour être précis seulement si (m+M).V=m.v où v est la vitesse du plomb et V la vitesse horizontale communiquée au pendule...". Mais je crois que la relation (m+M).V=m.v n'est autre que l'expression de la conservation de la quantité de mouvement, non?. Ceci revient à dire que la condition pour que la quantité de mouvement se conserve est qu'il ait conservation de la quantité de mouvement ??? S'agit-il d'un lapsus du clavier ou est-ce que je suis passé à coté de quelquechose ?
cordialement.
Pierre | |
|   | | Didier
Habitué Des Lieux


Nombre de messages : 326
Localisation : France Blois (41)
Date d'inscription : 31/05/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Jeu 10 Mai 2007 - 15:59 Jeu 10 Mai 2007 - 15:59 | |
| Non non ce n'est pas un lapsus... Effectivement si les percussions de réaction sont nulles alors la quantité de mouvement est conservée... Dans les équations figures les inconnues de réaction...
la condition qui doit être vérifiée pour que ces inconnues de réaction soient nulles est bien celle que j'ai écrite mais attention pour bien comprendre il faut bien voir que pour une masse m et vitesse v il faudrait avoir la bonne masse M et la bonne inertie du pendule (longueur des ficelles etc...) afin que la vitesse V communiquée au pendule soit telle que : m.v=(m+M).V
Et que en effet par le plus grand des miracles il y ai conservation de la quantité de mouvement... Bref c'est impossible de construire le pendule puisqu'il faudrait connaitre ce qu'on cherche à mesurer à savoir v... C'est sans issue ! Il faut revenir un pendule simple...
Je redis ici au cas où je n'aurais pas été clair la propriété de conservation de la quantité de mouvement n'est pas justement une "loi fondamentale" On peut la voir comme une conséquence des lois de Newton dans les cas particuliers de système mécanique isolé (ne subissant aucune action mécanique) ou pseudo isolé (subissant un ensemble d'action mécanique à somme nulle... C'est à dire s'annulant globalement les une les autres pour faire court...).
Somme des vecteurs forces = masse x vecteur accélération (théorème dit de la résultante dynamique)
autre écriture possible : somme des vecteurs force = dérivé par rapport au temps du vecteur quantité de mouvement...
et donc si la somme des forces est nulle et bien la dérivé du vecteur quantité de mouvement est nulle ce qui signifie qu'il est constant... Et quand le vecteur quantité de mouvement est constant cela revient à dire qu'il y a conservation de la quantité de mouvement...
Bon et puis c'est la moitié des données il faut écrire la même chose avec les vecteurs moment (théorème du moment dynamique)... qui conduit à la conservation du moment cinétique si la somme des vecteurs moment est nulle...
Le probleme avec ce pendule à deux fils c'est que la sommes des actions mécanique de liaison crée des percussions qui n'ont aucune raison de s'annuler mutuellement... Sauf si le rapport des masses et des vitesses est dans le rapport que j'ai indiqué...
D'où les essais que je te propose de faire... Qui devrait te conduire à mesurer des vitesses différentes soit lorsque tu modifie M soit lorsque tu modifie la longueur des fils...
Tu ne t'en est pas rendu compte parce que tes résultats étaient plausibles... Parce que dans ton cas les percussions de réaction ne sont pas trop forte... Si Loulator viens chez toi tu obtiendra comme lui des résultats très éloignés... Auras tu le temps de faire un ou deux mesures pour vérifier ?
Dernière édition par le Ven 11 Mai 2007 - 16:22, édité 1 fois | |
|   | | Pierre
Intermédiaire



 
Nombre de messages : 97
Age : 78
Localisation : Toulouse
Date d'inscription : 04/04/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Ven 11 Mai 2007 - 13:51 Ven 11 Mai 2007 - 13:51 | |
| Didier, Tu as probablement raison, et il faudra bien clore un jour cette discussion, mais je ne suis pas encore totalement convaincu et je souhaiterais approfondir encore en peu. Par le raisonnement et les calculs que je développe plus bas, j'ai l'impression quand même que les percussions de réactions sont nulles dans le pendule à 2 fils. Plus précisément, je montre que les percussions de réaction sont nulles en projection sur l'axe horizontal X, et que la somme de leurs moments est nulle aussi. On en déduit ensuite qu'il y a conservation de la quantité de mouvement pour ce qui concerne les composantes selon l'axe X. Je me trompe peut-être quelque part, dis moi ce que tu en penses. HYPOTHESES ET NOTATIONS - Je note comme toi m et v la masse et la vitesse du plomb, M et V la masse et la vitesse du pendule après la percussion. v et V sont des vecteurs. - Les deux fils en position de repos sont parallèles, verticaux, et de longueurs égales. Soit L la longueur de chaque fil. - Le plan vertical défini par les deux fils est supposé être un plan de symétrie du système. Le centre de gravité G du pendule est dans ce plan. Le vecteur v (vitesse du plomb) est supposé parfaitement horizontal et contenu dans ce plan, et il passe par le centre de gravité du pendule. - Moyennant ces hypothèses, le problème peut se décrire entièrement dans ce plan vertical (aucune force ne pointe en dehors du plan). Appelons XY ce plan, X étant l'axe horizontal et Y l'axe vertical. La trajectoire du plomb avant percussion est confondue avec l'axe X. - Maintenant, une hypothèse très importante : les fils sont supposés de masse négligeable, et surtout ils sont infiniment souples (la raideur en flexion des fils est nulle). --> comme les fils n'ont pas de raideur en flexion, les forces exercées par les fils aux points d'attache sur le pendule sont obligatoirement dirigées selon la direction du fil, à chaque instant. A l'instant de la percussion en particulier, les fils sont verticaux, et donc les percussions de réaction, si elles existent, sont nécessairement verticales. Il ne peut pas y a avoir une réaction à composante horizontale.DIFFERENTS TYPES DE PENDULES Limitons nous aux 3 types de pendules suivant : - a) Pendule suspendu par un bras rigide articulé sur un pivot. Le bras est suposé "soudé" au corps du pendule. C'est ce type de pendule qui est traité dans le site de Fréderic Elie dont tu avais fourni le lien: http://fred.elie.free.fr/pendule_balistique.htm - b) Pendule à un seul fil. - c) Pendule à deux fils (celui que j'ai essayé). 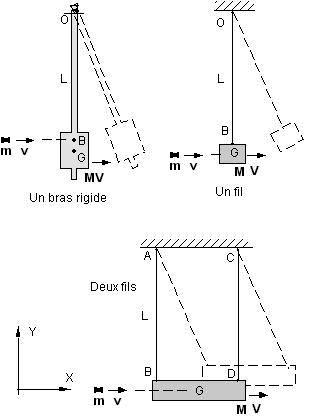 Ces 3 pendules ont des propriétés très différentes : 1) Tout d'abord, les percussions de réaction dans les pendules à 1 fil ou à 2 fils ne peuvent pas avoir de composante de composante horizontale, à cause de la souplesse des fils. Ce n'est pas du tout le cas pour le pendule à bras rigide : on a un bras raide articulé en O sur un pivot dur, et rien n'interdit qu'il y ait une percussion de réaction horizontale au niveau du pivot. C'est effectivement ce que montre Fred Elie : la réction en O n'est nulle que si le plomb percute le pendule en un point B très particulier, qui n'est pas le centre de gravité. Si le plomb percute plus haut (plus près de O) on a une réaction vers l'arrière au niveau du pivot, et inversement s'il percute plus bas. 2) Absence de moment cinétique propre dans le pendule à deux fils : c'est une différence fondamentale entre le pendule à deux fils et les deux autres pendules : dans les pendules à 1 bras ou à 1 fil, le corps du pendule décrit un mouvement de rotation autour de 0 après la percussion. Ce mouvement est assimilable à la superposition de deux mouvements : une translation du centre de gravité selon un arc de cercle, plus une rotation autour de G. Le moment cinétique propre du corps (autour de G) n'est pas nul après la percussion. Le cas du pendule à 2 fils est très différent de ce point de vue : en effet, la géométrie des deux fils fait que le pendule se translate en restant parallèle à lui-même, sans aucune rotation. Le moment cinétique autour de G est donc nul, par construction. CALCUL DES PERCUSIONS DE REACTION DANS LE PENDULE A 2 FILS : On considère ici le système constitué par le pendule seul. Sa quantité de mouvement est nulle avant la percussion, et elle devient (M+m)V après. Notons au passage que la cinématique du pendule est telle que la vitesse intiale V est orienté selon X, sans composante verticale. La loi des chocs dit que la variation de la quantité de mouvement est égale à la somme des vecteurs percussions au moment de l'impact du plomb. Il y a 3 percussions à considérer : - le vecteur percussion du plomb, orienté selon l'axe X, passant par G, et de module mv. - les deux percussions de réaction appliquées aux points d'attache des fils. Soient P1 et P2 ces deux vecteurs. Pour les raisons mentionnées plus haut, les vecteurs P1 et P2 sont dirigés selon l'axe vertcal Y, sans aucune composante selon X. On ne sait rien à ce stade sur les module et le sens de P1 et P2. La lois des chocs s'écrit alors : (M+mV) = mv + P1 + P2 où tous les termes sont des vecteurs. La même loi s'applique bien sur aux projections de ces vecteurs sur l'axe X. mais comme P1 et P2 sont perpendiculaires à X, leurs projections sur X sont nulles. On a donc bien (M+m)V = mv (CQFD)VARIATION DU MOMENT CINETIQUE : Calculons le moment cinétique du pendule autour du centre de gravité G : Il est bien sûr nul avant la percussion, mais on a vu plus haut qu'il reste nul aussi après la percussion puisqu'il n'y a aucune rotation autour de G. Donc la variation de moment cinétique est nulle. Cette variation (nulle) est égale à la somme des moments des percussions par rapport à G : - le moment de la percussion du plomb est nul puisque l'impact a lieu en G - comme le moment cinétique reste nul, il faut donc que : (moment de P1 + moment de P2) = 0 (CQFD)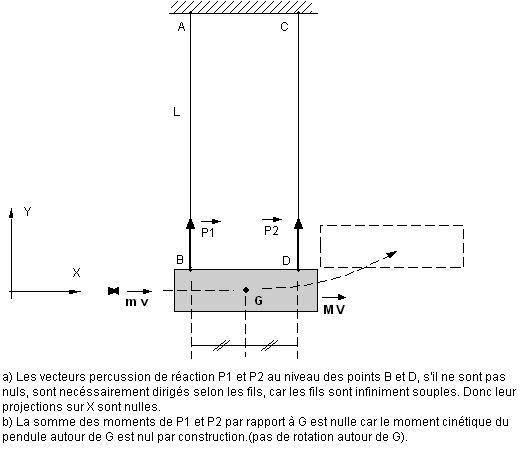 On peut encore affiner notre connaissance de P1 et P2. En effet, si G est équidistant des points d'attache comme sur la figure ci dessus, la somme des moments en G ne peut être nulle que si P1 et P2 sont de même module et de même sens (orientées vers le haut par exemple), c'est à dire P1=P2. Mais on ne peux rien dire de plus à ce stade sur le module commun de P1 et P2. Ce module est peut-être nul, ou pas, mais ça n'a pas d'importance ici. Voila, il me semble que le raisonnement est correct. Le truc pour arriver à ce résultat, c’est de bien prendre en compte les conditions cinématiques imposées par construction (déplacement sans rotation) et les contraintes physiques : fil souples --> réaction dirigée selon le fil. Si c'est correct, il restera à expliquer pourquoi Loulator a trouvé un résultat aberrant. Je ne peux pas faire d’investigations expérimentale à court terme : j'avais réalisé ce pendule il y a 6 mois, et je ne l'ai pas conservé : mon atelier est déjà bien encombré par d'innombrables bidules, et je ne peux pas tout garder. Cordialement. Pierre | |
|   | | Invité
Invité

 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Ven 11 Mai 2007 - 15:37 Ven 11 Mai 2007 - 15:37 | |
| Salut à tous
Salut Pierre
Je me suis renseigné sur le pendule balistique et effectivement il permet de mesurer avec une grande précision la vitesse du projectile et il ne sert pas uniquement à comparer la puissance des armes à feu comme je le pensais .
En cas de choc mou l'équation : m1v1=(m1+m2)v' équation (1)
m1 : masse du plomb
m2 : masse du pendule
v1 : vitesse du plomb avant le choc
v' : vitesse de l'ensemble (plomb+pendule) après le choc
Est valable qu'il y'ait déformation ou pas . Je me suis donc trompé de penser qu'il faudrait qu'une certaine quantité de mouvement responsable de déformation figure dans cette équation .
J'ai bien réfléchi à tout cela et je crois finalement comprendre pourquoi je suis tombé dans l'erreur et Pierre en est responsable en partie . Je m'explique :
Pierre et moi nous étions d'accord sur le fait qu'il y'a perte d'énergie cinétique du plomb en entraînant la déformation de la pâte à modeler (trou creusé sur la pâte) et sur le fait que l'énergie cinétique du projectile n'est pas complètement transmise au pendule à cause de la deformationj de la pate à modeler . nous pensions que :
Ec plomb = énergie responsable de déformation de pâte +Em du pendule
équation (2)
Ec : énergie cinétique du plomb avant choc
Em : énergie mécanique du pendule après le choc
Essayons de faire sortir v' de l'équation (1) dans l'équation (2) :
Em = Ec du pendule + Ep du pendule équation (3)
= 1/2 mv2 + m gh
m : masse du pendule
v : vitesse du pendule Ep : energie potentiel
soit (x'ox) l'horizontale passant par le centre de gravité du pendule quand il est au repos .
soit (y'oy) la verticale passant par le centre de gravité du pendule quand il est au repos .
h: hauteur qui sépare (x'ox) du centre de gravité du pendule.
quand le pendule oscille il décrit un arc .
lorsque le pendule oscille h et v varient de façon inverse . Quand h augmente v diminue et inversement .
quand le pendule atteint l'amplitude maximale h est maximale et v est nulle .
l'équation (3) s'écrit alors Em = 0 + mgh
C'est la mesure de h par des calculs géométriques qui permet de calculer l'énergie mécanique du pendule .
Quand le centre de gravité du pendule passe par (y'oy) :
L'équation (3) s'ecrit : Em pendule = 1/2 mv2 + mgh
h=0 ---------) Em= 1/2 mv2
Dans cette position l'énergie mécanique du pendule est égale à son énergie cinétique et la valeur de v dans cette position est la même valeur v' dans
l'équation (1) . v'= m1/(m1+m2)v
L'équation (2) :
Ec plomb = énergie responsable de déformation de pâte +Em du pendule
équation (2)
peut s'écrire alors:
1/2 mv12 = énergie responsable de déformation de pâte + 1/2 (m1+m2)v'2
car après le choc la masse du pendule = m1+m2
Dans l'équation (2) : v' dépend d'une certaine quantité d'énergie perdue en entraînant la déformation de la pâte à modeler .
Dans l'équation (1) ( raisonnement par conservation de quantité de mouvement en cas de choc mou ) : v' ne dépend pas de la déformation de la pâte .
Il y'a donc un problème :
L'une des deux équations est fausse .
Avant je pensais que c'est dans l'équation (1) qu'il y'a un problème . je croyais que cette équation n'est valable que si les deux corps ne sont pas déformables . Je pensais alors qu'il fallait qu'une certaine quantité de mouvement responsable de déformation y figure et cela pour que les deux équations soient valables toutes les deux . Mais je crois que c'est l'inverse . C'est dans l'équation (2) qu'il y'a un problème :
Ec plomb = énergie responsable de déformation de pâte + 1/2 (m1+m2)v'2
Je pense que nous nous somme trompés Pierre et moi en pensant qu'il y'a perte d'energie cinetique .
La pâte à modeler fait partie du pendule . en la creusant le plomb donne du mouvement au pendule . Il n'y'a pas donc de perte d'énergie cinétique mais plutôt un transfert de cette énergie au pendule . l'énergie cinétique du plomb avant le choc est pratiquement égale à l'énergie mécanique du pendule et cela indépendamment de la déformation de la pâte à modeler .
IL peut peut etre y'avoir une perte sous forme de chaleur ?.
Je pense donc que notre équation :
Ec plomb = énergie responsable de déformation de pâte +Em du pendule
équation (2)
est fausse . on devrait la remplacer par l'équation suivante :
Ec plomb = Em pendule --------)
1/2 m1v12 = 1/2 (m1+m2)v'2 ---------)même chose que équation (1) dans la quelle on a raisonné par la conservation de quantité de mouvement.
Sans tenir compte de la déformation de la pâte à modeler .
Autrement dit : il y'a en même temps conservation de l'énergie cinétique et de la quantité de mouvement dans le pendule balistique .
Pierre je crois maintenant que tu comprends pourquoi je me suis mis à inventer des équations et a me douter de la fiabilité du pendule balistique !!! c'est a cause de ce détail auquel en a pas bien fait attention . Nous nous sommes tromper de penser qu'il y'à perte de l'énergie cinétique a cause de la déformation de la pâte à modeler . Si tu es d'accord avec moi le problème est résolu .
A+ |
|   | | Didier
Habitué Des Lieux


Nombre de messages : 326
Localisation : France Blois (41)
Date d'inscription : 31/05/2005
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Ven 11 Mai 2007 - 15:58 Ven 11 Mai 2007 - 15:58 | |
| Pour moi aussi la discussion est close... En je suis maintenant de ton avis Pierre... Je ne voulais pas accepter l'hypothèse intuitive de l'absence de composante de percussion horizontale... Car cette hypothèse implique la nullité des composantes de percussion sur y également... Et ça ça me perturbait.
J'ai bien les mêmes relation que toi... Et elles permettent de conclure alors que la totalité des composantes de percussion sont nulles... Et c'était bien là mon soucis... Faire l'hypothèse qu'il n'y à pas de percussion sur x c'est admetre qu'il n'y en a pas non plus sur y...
Il me reste donc juste une précision à apporter pour compléter ta demonstration... Au sujet des composantes de percussion sur y :
théorème de la résultante:
sur x : (m+M).V-m.v=0 (1)
sur y : Y1+Y2=0 (2) avec Y1 et Y2 les composantes sur y des vecteurs percussion.
Théorème du moment (somme des moments en G) :
sur z : -Y1+Y2=0 (3)
Donc en vertu de (2) et (3) Y1=Y2=0 puisque les composantes sont à la fois égales entre elles et opposées entre elles...
Donc il y a conservation de la quantité de mouvement.
Et le mystère Loulator reste entier !
Merci encore Pierre pour cet échange qui m'a permis d'y voir plus clair sur un sujet que je n'avais pas abordé depuis une bonne dizaine d'année... | |
|   | | zac
Pilier



 
Nombre de messages : 1231
Age : 55
Localisation : Volckerinckhove
Date d'inscription : 29/03/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Ven 11 Mai 2007 - 16:57 Ven 11 Mai 2007 - 16:57 | |
| Eureka!!!
bon sans blague, j'ai survolé votre débat, c'est très intéressent.
mais n'y aurai t-il personne sur le forum, qui possèdent un chronographe et qui réaliserait un pendule balistique via le indication de pierre et qui comparerai avec les valeurs de sont chronographe, comme cela on aurai une idée, si c'est viable ou pas?
sinon, c'est ça l'oscillation verticale:
http://www.univ-lemans.fr/enseignements/physique/02/meca/balistique.html | |
|   | | Pierre
Intermédiaire



 
Nombre de messages : 97
Age : 78
Localisation : Toulouse
Date d'inscription : 04/04/2006
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  Sam 12 Mai 2007 - 4:51 Sam 12 Mai 2007 - 4:51 | |
| Réponses à Tous :
Didier
Cette fois c’est bon, nous sommes d’accord sur tout : le principe du pendule balistique à deux fils est correct, et il y a bien conservation de la quantité de mouvement. Les résultats trouvés par Loulator restent donc un mystère pour l’instant.
Merci pour cette discussion, qui a été pour moi aussi un plaisir.
Zac
J’ai fait la comparaison pendule/chronographe pour ma carabine Diana-28, qui est donnée pour 235 m/s par le fabricant.
- Mesure au pendule, effectuée il y 6 mois avec des plombs de 0.5 g : 226 m/s
Ce résultat est la moyenne sur une dizaine de mesures qui se situaient dans une plage 202-230. Cette dispersion assez grande provient en partie de l’imprécision de la lecture du déplacement sur le mètre.
- Mesure avec un chronographe de marque « Chrony », prêté par un ami il y a quelques jours : 206 m/s. La dispersion des mesures au chronographe est très faible (plage 203-209).
Conclusion : le pendule balistique, ça marche en théorie, c’est sympa, mais si vous voulez des mesures vraiment précises il vaut mieux se payer un chronographe !
Khalid
J’ai bien lu ton dernier post et je suis heureux que tu arrives toi aussi à a conclusion que la quantité de mouvement se conserve dans un choc mou. Mais quand tu dis que l’énergie cinétique se conserve aussi, là je ne peux pas être d’accord.
Pour t’en convaincre, regarde l’ exemple numérique concret ci-dessous :
- masse du plomb : m = 1 gramme (0.001 kg)
- vitesse du plomb : v = 100 m/s
- masse du pendule : M = 1 kg
- vitesse du pendule après l’impact : V (inconnue)
Si tu admets la conservation de la quantité de mouvement, tu peux calculer V. tu trouveras V=0.1m/s.
Ensuite, calcule avec ces valeurs l’énergie cinétique du plomb et celle du pendule. Tu trouveras:
EC plomb = 5 joule
ECpendule = 0.005 joule
L’énergie cinétique du pendule est ici 1000 fois plus faible que celle du plomb, donc l’énergie cinétique ne se conserve pas dans le cas d’un choc mou. C’est comme ça, il n’y a rien à faire !
Au passage, on remarque sur ce cas particulier que les vitesses et les énergies cinétiques sont dans le même rapport, un rapport 1000 ici. En explicitant les relations littérales, on peut montrer que cette loi est générale lorsque la masse du plomb est très petite devant celle du pendule : on a alors :
V / v = EC pendule / ECplomb = m / M. (ce n’est plus vrai si les deux masses sont comparables).
Un peu de philosophie :
La majeure partie de l’énergie du plomb sert à déformer le plomb, la pâte à modeler, et le sable. Mais rien ne se perd : cette énergie de déformation se transforme ensuite en chaleur qui est une autre forme d’énergie.
Allons plus loin : après quelques minutes les oscillations du pendule s’arrêtent par frottement dans l’air, et qui dit frottement dit dégagement de chaleur : à la fin tout est immobile, toute l’énergie du plomb s’est transformée en chaleur, et la température de l'air dans la pièce ou se trouve le pendule s'est un peu élevée.
Allons encore plus loin : pour les physiciens, la température d'un objet est due à l'agitation thermique des atomes qui le constituent. L'énergie thermique (ou chaleur) contenue dans un obet n'est autre que l'énergie cinétique de tous ses atomes. Quant on apporte de la chaleur à un objet on augmente l'agitation de ses atomes et donc on augmente leur énergie cinétique (dans le langage courant on dit que l'on a échauffé l'objet).
Sous cet aspect là, on peut dire que toute l'énergie cinétique du plomb se transforme à la fin des fins en énergie cinétique des atomes de l'air. Il ya donc quelquepart conservation de l'énergie cinétique. Kahlid n'avait pas tort finalement...
Bon, il est bientôt midi, il fait beau, ça va être l'heure du Ricard...
Cordialement
Pierre | |
|   | | Contenu sponsorisé
 |  Sujet: Re: Mesure de vitesse au pendule balistique Sujet: Re: Mesure de vitesse au pendule balistique  | |
| |
|   | | | | Mesure de vitesse au pendule balistique |  |
|
Sujets similaires |  |
|
| | Permission de ce forum: | Vous ne pouvez pas répondre aux sujets dans ce forum
| |
| |
| |
